PMT Pulse analysis

Jelle, updated May 2019

updated Feb 2022 by Joran

Standard python setup:

import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt

# This just ensures some comments in dataframes below display nicely
import pandas as pd

pd.options.display.max_colwidth = 100

After this standard setup, we can load straxen:

import strax
import straxen

st = straxen.contexts.xenonnt_online()
straxen.print_versions()

cutax is not installed

	module	version	path	git
0	python	3.10.0	/home/angevaare/miniconda3/envs/dev_strax/bin/python	None
1	strax	1.1.7	/home/angevaare/software/dev_strax/strax/strax	branch:master | db14f80
2	straxen	1.2.8	/home/angevaare/software/dev_strax/straxen/straxen	branch:master | 024602e

Raw records

Let’s select a run for which we have strax data.

dsets = st.select_runs(
    available="raw_records",
)
run_id = dsets.name.min()
run_id

'008334'

st.storage

[straxen.storage.rundb.RunDB, readonly: True,
 strax.storage.files.DataDirectory, readonly: True, path: /dali/lgrandi/xenonnt/raw, take_only: ('raw_records', 'raw_records_he', 'raw_records_aqmon', 'raw_records_nv', 'raw_records_aqmon_nv', 'raw_records_aux_mv', 'raw_records_mv'),
 strax.storage.files.DataDirectory, readonly: True, path: /dali/lgrandi/xenonnt/processed,
 strax.storage.files.DataDirectory, path: ./strax_data]

This run is one hour long, so the full raw waveform data won’t fit into memory. Let’s instead load only the first 30 seconds:

rr = st.get_array(run_id, "raw_records", seconds_range=(0, 30))

convert_channel::       changed channel
convert_channel::       changed channel
convert_channel::       changed channel
convert_channel::       changed channel
convert_channel::       changed channel
convert_channel::       changed channel

The rr object is a numpy record array. This works almost like a pandas dataframe, in particular, you can use the same syntax you’re used to from dataframes for selections.

Here are the fields you can access:

st.data_info("raw_records")

	Field name	Data type	Comment
0	time	int64	Start time since unix epoch [ns]
1	length	int32	Length of the interval in samples
2	dt	int16	Width of one sample [ns]
3	channel	int16	Channel/PMT number
4	pulse_length	int32	Length of pulse to which the record belongs (without zero-padding)
5	record_i	int16	Fragment number in the pulse
6	baseline	int16	Baseline determined by the digitizer (if this is supported)
7	data	('<i2', (110,))	Waveform data in raw ADC counts

You now have a matrix (record_i, sample_j) of waveforms in rr[‘data’]:

rr["data"].shape

(3046781, 110)

Let’s select only records that belong to short PMT pulses. These are mostly lone PMT hits. Longer pulses are likely part of S1s or S2s.

rr = rr[rr["pulse_length"] < 110]

Here’s one record:

def plot_record(sample_r):
    plt.plot(sample_r["data"][: sample_r["length"]], drawstyle="steps-mid")
    plt.xlabel("Sample number")
    plt.ylabel("Amplitude (ADCc)")


sample_r = rr[0]
plot_record(sample_r)

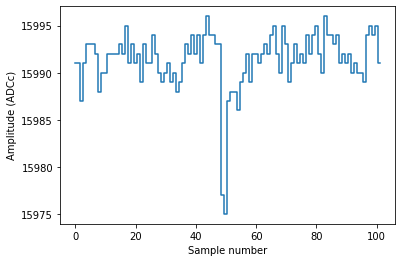
As you can see, this record contains a single PE pulse, straight as it comes off the DAQ. No operations have been done on it; we did not even subtract the baseline and flip the pulse.

Each record is 110 samples long, but this digitizer pulse was only 102 samples long:

sample_r["pulse_length"]

102

and thus the pulse has been zero-padded:

sample_r["data"]

array([15991, 15991, 15987, 15991, 15993, 15993, 15993, 15992, 15988,
       15990, 15990, 15992, 15992, 15992, 15992, 15993, 15992, 15995,
       15991, 15993, 15991, 15992, 15989, 15993, 15991, 15991, 15994,
       15992, 15990, 15989, 15990, 15991, 15989, 15990, 15988, 15989,
       15991, 15993, 15992, 15994, 15992, 15994, 15991, 15994, 15996,
       15994, 15994, 15993, 15993, 15977, 15975, 15987, 15988, 15988,
       15986, 15989, 15990, 15992, 15989, 15992, 15992, 15991, 15992,
       15993, 15992, 15994, 15995, 15992, 15990, 15995, 15993, 15989,
       15991, 15993, 15991, 15992, 15991, 15994, 15992, 15994, 15995,
       15992, 15990, 15996, 15994, 15994, 15993, 15994, 15991, 15992,
       15991, 15992, 15990, 15991, 15990, 15990, 15989, 15994, 15995,
       15994, 15995, 15991,     0,     0,     0,     0,     0,     0,
           0,     0], dtype=int16)

Let’s take care of the baseline and zero padding:

# Convert from raw_records to the records datatype, which has more fields.
# Without this we cannot baseline.
rr = strax.raw_to_records(rr)

# Subtract baseline and flip channel
strax.baseline(rr)

Now things look more reasonable:

plot_record(rr[0])

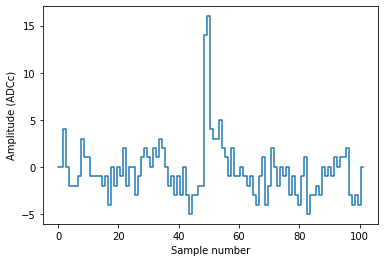
Pulse shape

Let’s focus on channel 100:

r = rr[rr["channel"] == 100]

Here is the distribution of amplitudes in each sample. This is very roughly the mean pulse shape:

ns = np.arange(len(r[0]["data"]))

plt.plot(ns, r["data"].mean(axis=0), drawstyle="steps-mid")
plt.fill_between(
    ns,
    np.percentile(r["data"], 25, axis=0),
    np.percentile(r["data"], 75, axis=0),
    step="mid",
    alpha=0.3,
    linewidth=0,
)
plt.xlabel("Sample in record")
plt.ylabel("Amplitude (ADCc)")

Text(0, 0.5, 'Amplitude (ADCc)')

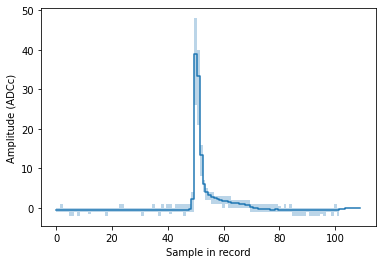
You can clearly see we’re dealing with single PEs here, and also see the infamous long PE pulse tail. For a serious pulse shape study you should of course first normalize the pulses.

Gain calibration

run_id

'008334'

Let’s integrate between sample 40 and 70, to get the mean single-PE area. We have to add a small correction for the baseline, see here for details. Usually this is done inside strax and you don’t have to worry about it.

left, right = 40, 70
areas = r["data"][:, left:right].sum(axis=1)

# Small correction for baseline, see strax issue #2
areas += ((r["baseline"] % 1) * (right - left)).round().astype(np.int64)

# Hack to get ADC -> PE conversion factors. We'll make this better someday...
to_pe = st.get_single_plugin(run_id, "peaklets").to_pe

plt.hist(areas, bins=100)
plt.xlabel("Area (ADCc)")
plt.ylabel("Counts")
plt.axvline(1 / to_pe[100], color="r", linestyle="--")
plt.axvline(np.median(areas), color="purple", linestyle="--")

<matplotlib.lines.Line2D at 0x7fb99a612950>

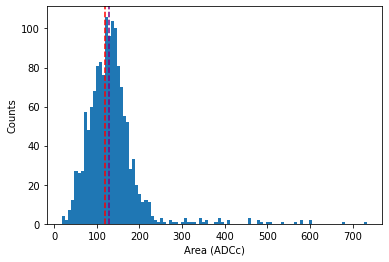
The purple line is an extremely bad gain estimate (the median area) of pulses, which nonetheless comes close for this PMT. It should be obvious this is a bad method: it takes no account of 2PE hits or the hitfinder efficiency at all.

The red line indicates where the 1 PE area should be according to the XENON1T gain calibration. Looks like the gain is, at least approximately, correct!

Let’s do the same for all PMTs:

areas = rr["data"][:, 40:70].sum(axis=1)
channels = rr["channel"]

gain_ests = np.array(
    [np.median(areas[channels == pmt]) for pmt in tqdm(np.arange(straxen.n_tpc_pmts))]
)

  2%|▏         | 12/494 [00:00<00:16, 29.33it/s]/home/angevaare/miniconda3/envs/dev_strax/lib/python3.10/site-packages/numpy/core/fromnumeric.py:3440: RuntimeWarning: Mean of empty slice.
  return _methods._mean(a, axis=axis, dtype=dtype,
/home/angevaare/miniconda3/envs/dev_strax/lib/python3.10/site-packages/numpy/core/_methods.py:189: RuntimeWarning: invalid value encountered in double_scalars
  ret = ret.dtype.type(ret / rcount)
100%|██████████| 494/494 [00:18<00:00, 27.23it/s]

plt.scatter(1 / to_pe, gain_ests, s=2)
plt.plot([0, 250], [0, 250], c="k", alpha=0.2)
plt.xlabel("XENONnT gain calibration (ADCc)")
plt.ylabel("Median short pulse area (ADCc)")
plt.title("Pulse areas in ADCc for each PMT")
plt.xlim(left=0)
plt.ylim(bottom=0)
plt.gca().set_aspect("equal")

/tmp/jobs/17887550/ipykernel_29675/2656599034.py:1: RuntimeWarning: divide by zero encountered in true_divide
  plt.scatter(1/to_pe, gain_ests, s=2)

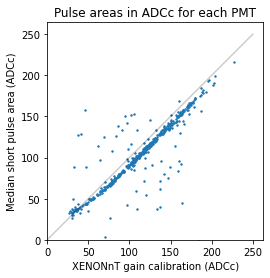
As you can see, even this extremely basic method (median area of short pulses in 30sec of background data) gives a somewhat plausible gain estimate for most PMTs.